Khi nghiên cứu cực trị địa phương của các hàm nhiều biến, ví dụ quen thuộc là xét hàm đa thức
P(x,y)=x2+3xy+3y2−6x+3y−6.
Ta có Px=2x+3y−6 và Py=3x+6y+3 , nên điểm dừng của P là (15,−8). Vì ′Pxx=2 và Hessian của P bằng 2×6−32=3>0 , nên ′(15,−8) là điểm cực tiểu của P , giá trị cực tiểu bằng P(15,−8)=−63.
P là đa thức, người ta hy vọng có một giả thíc đại số tại sao −63 là cực tiểu của nó và tại sao lại đạt được tại (15,−8) . Đối với hàm một biến: Nếu p(x)=ax2+bx+c và a>0 thì
p(x)=a(x+b2a)2+4ac−b24a,
do đó p đạt cực tiểu tại x=−b/2a ,và giá trị cực tiểu là (4ac−b2)/4a.
Đa thức P ở trên cũng có thể biểu diễn theo cách này. Một chút tính toán đại số cho ta
Đa thức P ở trên cũng có thể biểu diễn theo cách này. Một chút tính toán đại số cho ta
P(x,y)=(x−3+32y)2+3(y2+4)2−63, >
và giá trị nhỏ nhất của P(x,y) là −63 , đạt được khi x−3+3y/2=0 và 4+y/2=0 , tức là tại (15,−8) .
(Ta có thể giải thích phân tích củaP ở trên bằng một thuật toán, nhưng ta tạm bỏ qua.)
Phân tích ở trên củaP không chỉ là một sự trùng hợp. Bài toán thứ 17 trong 23 bài toán của Hilbert tại Đại hội Toán học Thế giới lần 2 ở Paris, 1900 phát biểu rằng liệu mọi đa thức với hệ số thực  không âm với mọi giá trị
không âm với mọi giá trị  là tổng các bình phương (gọi tắc là SOS) của các hàm số hữu tỉ. (Một hàm số hữu tỉ là thương của các đa thức.) Một đa thức như trên thường được gọi là xác định dương .
là tổng các bình phương (gọi tắc là SOS) của các hàm số hữu tỉ. (Một hàm số hữu tỉ là thương của các đa thức.) Một đa thức như trên thường được gọi là xác định dương .
Nếu bài toán của Hilbert cho câu trả lời khẳng định, nó sẽ cho một lời giải thích rõ ràng tại sao P không âm. Chính Hilbert chứng minh rằng một đa thức không âm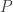 là tổng các bình phương của các đa thức khi thuộc một trong các trường hopwj sau đây:
là tổng các bình phương của các đa thức khi thuộc một trong các trường hopwj sau đây:
(Ta có thể giải thích phân tích của
Phân tích ở trên của
Nếu bài toán của Hilbert cho câu trả lời khẳng định, nó sẽ cho một lời giải thích rõ ràng tại sao P không âm. Chính Hilbert chứng minh rằng một đa thức không âm
là đa thức một biến,
là đa thức bậc hai n biến,
là đa thức bậc bốn hai biến.
Emil Artin đã giải bài toán Hilbert vào năm 1927 với câu trả lời khẳng định. Kết quả mạnh hơn, P là tổng các bình phương của các đa thức thật đáng tiếc là không đúng trong trường hợp tổng quát. Sau đây là một phản thí dụ:
Đa thức này không âm theo bất đẳng thức AM-GM (xem ví dụ 1 bên dưới). Đa thức này xuất hiện trong bài báo của Marie-Francoise Roy, The role of Hilbert’s problems in real algebraic geometry, ở tạp chí Proceedings of the ninth EWM Meeting, Loccum, Germany 1999, và ta có thể chứng minh rằng nó không phảo là tổng bình phương của các đa thức bằng thuật toán được giới thiệu bên dưới.
Mặc dù Hilbert đã biết một số đa thức không âm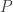 không là tổng bình phương các đa thức nhưng ví dụ tường minh đầu tiên cho thấy một đa thức như vậy thuộc về nhà logic học Rafael Robinson trong bài báo Some definite polynomials which are not sums of squares of real polynomials, in Selected questions of algebra and logic(collection dedicated to the memory of A. I. Mal′cev) (Tiếng Nga), pp. 264-282, Izdat.‘‘Nauka’’ Sibirsk.Otdel.,Novosibirsk, 1973.
không là tổng bình phương các đa thức nhưng ví dụ tường minh đầu tiên cho thấy một đa thức như vậy thuộc về nhà logic học Rafael Robinson trong bài báo Some definite polynomials which are not sums of squares of real polynomials, in Selected questions of algebra and logic(collection dedicated to the memory of A. I. Mal′cev) (Tiếng Nga), pp. 264-282, Izdat.‘‘Nauka’’ Sibirsk.Otdel.,Novosibirsk, 1973.
Ta trích dẫn bình luận trên Mathscinet của W. Ellison:
Mặc dù Hilbert đã biết một số đa thức không âm
Ta trích dẫn bình luận trên Mathscinet của W. Ellison:
Chìa khóa của vấn đề là bổ đề sau: Một đa thứccó bậc tối đa bằng 3 triệt tiêu tại 8 trong 9 điểm
với
phải triệt tiêu tại điểm thứ 9.
Đa thứctriệt tiêu tại 9 điểm này và ta có thể tìm một đươngc cong bậc 6
không đi qua
nhưng triệt tiêu tại 8 điểm còn lại ví dụ như
Hàm
bị chặn trên trên mặt phẳng
plane. Do đó với
thích hopwj (thật ra ta có thể chọn
) ta có
xác định dương và
Rõ ràng ta không thể có
với
là các đa thức hệ số thực, với bậc cao nhất bằng 3 và nó sẽ triệt tiêu tại
vì nó triệt tiêu tại 8 điểm khác.
Hơn nữa còn có một thuật toán cho vấn đề này, cho một đa thức không âm, có hay không một biểu diễn thành tổng các bình phương và nếu có, hãy tìm nó. Đây là kết quả chính của bài báo An algorithm for sums of squares of real polynomials, của Victoria Powers và Thorsten Woermann, J. Pure and Appl. Alg. 127 (1998), 99-104. (Bài báo này có tại trang web của Powers)
Nhiều bất đẳng thức thường gặp trong giải tích có thể chứng minh một cách hiệu quả dựa vào các đa thức không âm.
Nhiều bất đẳng thức thường gặp trong giải tích có thể chứng minh một cách hiệu quả dựa vào các đa thức không âm.
Tiếp theo phần 1
1. Bất đẳng thức AM-GM
1. Bất đẳng thức AM-GM
với mọi số không âm
Điều này tương đương với đa thức
được phân tích thành tổng các bình phương. Ở đây ta thay
Một phân tích như vậy được đưa ra bởi Hurwitz vào năm 1891,trong bài báo Über den Vergleich des arithmetischen und des geometrischen Mittels, có thể tìm đọc trong Math. Werke, 505-507, Basel, E. Berkhäuser, 1933.
Để bieur diễn được đẹp mắt hơn, ta đưa ra một số kí hiệu. Cho hàm số
Chẳng hạn,
Ta viết
với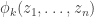
Lư ý rằng mỗi
Khi đó
Dấu bằng xảy ra nếu
Ví dụ,
và
2. Bất đẳng thức Cauchy-Schwarz
Dấu bằng xảy ra khi bộ n số 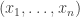 và
và  tỉ lệ. Chứng minh hay gặp của nó là dùng định thức của đa thức bậc hai không âm. Dạng đơn giản hơn của nó là
tỉ lệ. Chứng minh hay gặp của nó là dùng định thức của đa thức bậc hai không âm. Dạng đơn giản hơn của nó là  với
với  là các vector bất kì trong
là các vector bất kì trong 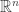 và
và  là tích vô hướng thông thường. Đặt
là tích vô hướng thông thường. Đặt
bất đẳng thức tương đương với đa thức 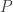 không âm, và có thể chứng minh bằng cách phân tích nó thành tổng các bình phương. Hằng đẳng thức Lagrange
không âm, và có thể chứng minh bằng cách phân tích nó thành tổng các bình phương. Hằng đẳng thức Lagrange
cho ta kết quả mong muốn.
3. Bất đẳng thức Young
Nếu p và q là các số hữu tỉ dương sao cho 1p+1q=1 , thì với mọi số dương x và y ta có
xpp+yqq≥xy.
Vì1p+1q=1 ,ta có thể viết p=m+nm , q=m+nn trong đó m và n là các số nguyên dương. Ta viết x=a1/p , y=b1/q . Khi đó
xpp+yqq=am+nm+bm+nn=ma+nbm+n.
Theo bất đẳng thức AM-GM,
ma+nbm+n≥(am⋅bn)1m+n=a1pb1q=xy, và do đó
xpp+yqq≥xy.
Chứng minh này xuất hiện trong cuốn Mathematical Toolchest xuất bản năm 2004 bởi Australian Mathematics Trust.
Vì
Theo bất đẳng thức AM-GM,
Chứng minh này xuất hiện trong cuốn Mathematical Toolchest xuất bản năm 2004 bởi Australian Mathematics Trust.
4. Bất đẳng thức Minkowski: Với các số không âm
Ta cần chứng minh đa thức sau không âm
Bạn đọc tự tìm hiểu.
Còn nữa...
Còn nữa...